DP 动态规划

0.动态规划三要素

1. 状态定义：由背包问题相关的变量描述的一个东西
   1. 定义状态往往是最难的一步，这决定了对问题整体的建模
   2. 例如状态可以是：“前 i 个物品在容量 j 下的最大价值”
   3. 定义好状态后，再由此给出状态转移方程
2. 状态转移方程：描述如何从一个状态到另一个状态
   1. 延续上面的状态定义，令dp[i][j]表示 “前 i 个物品在容量 j 下的最大价值”
   2. 那么如果是0-1背包，状态转移方程则是：dp[i][j] = max(dp[i-1][j], dp[i-1][j-w[i]] + v[i])
   3. 初始条件和边界(问题的最小规模下的解)
      1. 例如，在背包问题中，当没有物品或背包容量为0时，最大价值为0。

1.背包DP（用DP求解背包问题）

• 背包问题：给定一组物品，每个物品有重量和价值，在不超过背包容量的前提下，如何选择物品使总价值最大

  • 0-1背包：每种物品只有一个，选择放入(1)或不放入(0)背包

  //滚动数组优化：dp[j]表示j容量下的最大价值
  // 遍历每个物品
  for (int i = 0; i < n; i++) {
      // 从后往前遍历容量
      for (int j = W; j >= wt[i]; j--) {
          dp[j] = max(dp[j], dp[j - wt[i]] + val[i]);// 更新dp[j]
      }
  }
  

  • 完全背包：每种物品都有无限个

  //滚动数组优化：dp[j]表示j容量下的最大价值
  // 遍历每个物品
  for (int i = 0; i < n; i++) {
      // 从前往后遍历容量
      for (int j = wt[i]; j <= W; j++) {
          dp[j] = max(dp[j], dp[j - wt[i]] + val[i]);// 更新dp[j]
      }
  }
  

  小结：可以发现0-1背包和完全背包的差别其实就是一个倒序遍历一个正序遍历（正序遍历意味着可以选无限个，倒序则意味着只能选一个或者不选）

  • 多重背包：每种物品都有数量限制

      // 遍历每个物品
      for (int i = 0; i < n; i++) {
          // 遍历每种容量（从后往前）
          for (int j = W; j >= wt[i]; j--) {
              // 遍历当前物品的选择数量k
              for (int k = 1; k <= s[i] && k * wt[i] <= j; k++) {
                  dp[j] = max(dp[j], dp[j - k * wt[i]] + k * val[i]);
              }
          }
      }
  

  其实这个也是正序遍历，只不过相当于把第i种的k个看成了k种，转化为了0-1背包

  附：多重背包的二进制优化（?本质上是通过类似于以2为底的指数增长来更快的选完物品数量）

  for (int i = 0; i < n; i++) {
      // 二进制拆分
      int num = s[i]; // 当前物品的数量
      for (int k = 1; k <= num; k *= 2) {
          // 拆分出一个二进制分组
          int newWt = k * wt[i]; // 新物品的重量
          int newVal = k * val[i]; // 新物品的价值
          // 从后往前更新dp数组
          for (int j = W; j >= newWt; j--) {
              dp[j] = max(dp[j], dp[j - newWt] + newVal);
          }
          num -= k; // 减去已经拆分的数量
      }
      // 处理剩余的部分
      if (num > 0) {
          int newWt = num * wt[i];
          int newVal = num * val[i];
          for (int j = W; j >= newWt; j--) {
              dp[j] = max(dp[j], dp[j - newWt] + newVal);
          }
      }
  }
  

## 1.1 补充：记忆化搜索

- 记忆化搜索：一种通过记录已经遍历过的状态的信息，从而避免 对同一状态重复遍历的搜索实现方式。
- 因为记忆化搜索确保了每个状态只访问一次，它也是一种常见的 动态规划实现方式，一般基于dfs

```cpp
//基于dfs的记忆化搜索(vis数组就是“记忆”，表示这个状态的东西是否被访问过)
bool dfs(int n,int m){
    if(n<m)return 0;
    if(n==m)return 1;
    if(n%3!=0||vis[n])return 0;
    vis[n]=1;//加入记忆
    int p=n/3,q=p*2;
    return dfs(p,m)||dfs(q,m);
}

2.线性DP

• 线性 DP 不是某一种 DP , 而是一类 DP 的统称.
• 线性 DP 指转移的形式是线性的, 不是指复杂度是线性的.

2.1 一维

• 题目描述

• 给出一个长度为 n 的序列 a，选出其中连续且非空的一段使得这段和最大。

• 思路

• 首先定义dp[i] 表示只考虑前 i 个元素时, a[i] 所在的子段的最大和，然后题目所求的答案就是max(dp[1],dp[2]...dp[n])，初始状态dp[0]=0

• 状态转移方程：dp[i] = max(dp[i - 1] + a[i], a[i])即只考虑前i个元素时a[i]所在子段要么是它本身要么是他前一个加上他本身(因为dp[i]一定要包含a[i])

  dp[0] = 0;  // 初始条件
  for (int i = 1; i <= n; i++) {
      dp[i] = max(dp[i - 1] + a[i], a[i]);
  }
  int ans = -INF;
  for (int i = 1; i <= n; i++) {
      ans = max(ans, dp[i]);
  }

• 优化：滚动数组(减少掉一维，因为从头到尾只用到了dp[i]和dp[i-1])

int ans = -INF;
int sum = 0;
for (int i = 1; i <= n; i++) {
    sum = max(sum + a[i], a[i]);
    ans = max(ans, sum);
}

2.2 二维

• 题目描述

• 有一个n行m列的网格. 某人从左上角(1,1)出发, 前往右下角(n,m) ,若要求 每一步只能向下走或向右走, 且不能走入行数和列数都为偶数的格, 求他行进的方案数.

• 思路

  • 定义dp[i][j]表示从(1,1)到(i,j)的方案数，则答案为dp[n][m]
  • 状态转移方程dp[i][j]=dp[i-1][j]+dp[i][j-1](i,j不同时为偶数)
  • 初始条件dp[1][1]=1

for (int i = 1; i <= n; i++) {
    for (int j = 1; j <= m; j++) {
        if (i == 1 && j == 1) continue;
        if ((i & 1) || (j & 1)) {
            dp[i][j] = dp[i - 1][j] + dp[i][j - 1];
        }
    }
}

2.3 三维

• 题目描述

  • 某人带着2单位的酒出发, 一路上遇到店n次, 遇到花m次, 最后一次遇到的是花, 且正好将酒喝光. 已知他遇到店时, 拥有的酒量会翻一倍; 遇到花时, 拥有的酒量会减少1单位. 求他路上遇到店和花的顺序的方案数, 答案对(1e9+7)取模. 规定: 没有酒时遇到店是合法的, 但遇到花是不合法的.

• 思路

  • dp[i][j][k]表示走了i步，经过了j次店，当前酒量为k的方案数(即想要达成这样的状态可以有多少种花和店的排列)

  • 状态转移方程

    • 上一步遇到花dp[i][j][k]=dp[i][j][k]+dp[i-1][j][k+1]
    • 上一步遇到店dp[i][j][k]=dp[i][j][k]+dp[i-1][j-1][k/2]

  • 初始条件

    • dp[1][0][2]=1

  • 由题最后一次遇到的是花, 且正好将酒喝光，所以答案dp[n+m][n][1]

dp[1][0][2] = 1;  // 初始条件
for (int i = 2; i <= n + m; i++) {
    for (int j = 0; j <= n; j++) {
        for (int k = 0; k <= m; k++) {
            // 遇到花
            dp[i][j][k] = (dp[i][j][k] + dp[i - 1][j][k + 1]) % MOD;
            // 遇到店
            if (j && (k % 2 == 0)) {
                dp[i][j][k] = (dp[i][j][k] + dp[i - 1][j - 1][k / 2]) % MOD;
            }
        }
    }
}

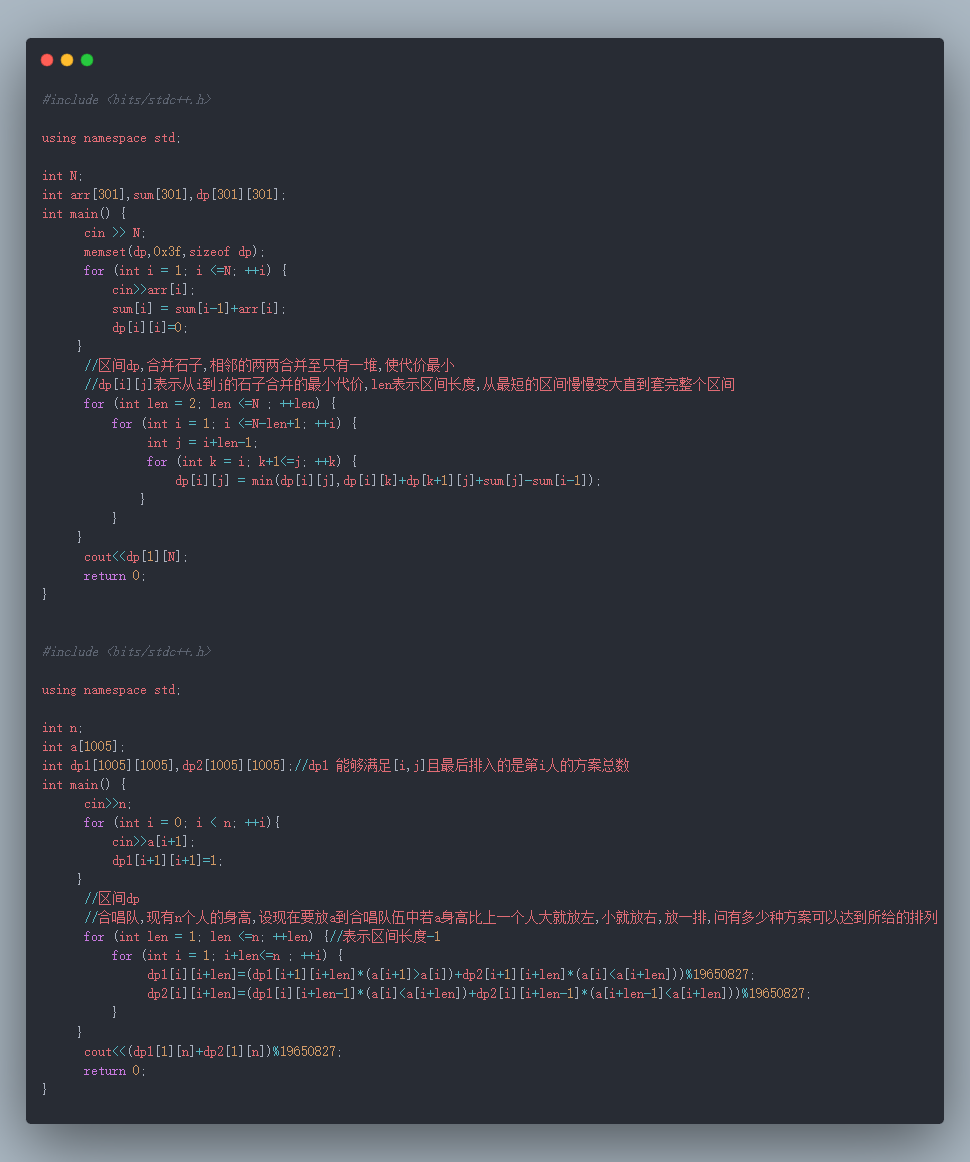
3.区间DP

#include <bits/stdc++.h>

using namespace std;

int N;
int arr[301],sum[301],dp[301][301];
int main() {
    cin >> N;
    memset(dp,0x3f,sizeof dp);
    for (int i = 1; i <=N; ++i) {
       cin>>arr[i];
       sum[i] = sum[i-1]+arr[i];
       dp[i][i]=0;
    }
    //区间dp,合并石子,相邻的两两合并至只有一堆,使代价最小
    //dp[i][j]表示从i到j的石子合并的最小代价,len表示区间长度,从最短的区间慢慢变大直到套完整个区间
    for (int len = 2; len <=N ; ++len) {
       for (int i = 1; i <=N-len+1; ++i) {
          int j = i+len-1;
          for (int k = i; k+1<=j; ++k) {
             dp[i][j] = min(dp[i][j],dp[i][k]+dp[k+1][j]+sum[j]-sum[i-1]);
          }
       }
    }
    cout<<dp[1][N];
    return 0;
}

#include <bits/stdc++.h>

using namespace std;

int n;
int a[1005];
int dp1[1005][1005],dp2[1005][1005];//dp1 能够满足[i,j]且最后排入的是第i人的方案总数
int main() {
    cin>>n;
    for (int i = 0; i < n; ++i){
       cin>>a[i+1];
       dp1[i+1][i+1]=1;
    }
    //区间dp
    //合唱队,现有n个人的身高,设现在要放a到合唱队伍中若a身高比上一个人大就放左,小就放右,放一排,问有多少种方案可以达到所给的排列
    for (int len = 1; len <=n; ++len) {//表示区间长度-1
       for (int i = 1; i+len<=n ; ++i) {
          dp1[i][i+len]=(dp1[i+1][i+len]*(a[i+1]>a[i])+dp2[i+1][i+len]*(a[i]<a[i+len]))%19650827;
          dp2[i][i+len]=(dp1[i][i+len-1]*(a[i]<a[i+len])+dp2[i][i+len-1]*(a[i+len-1]<a[i+len]))%19650827;
       }
    }
    cout<<(dp1[1][n]+dp2[1][n])%19650827;
    return 0;
}